Непрерывность функции в точке и на множестве. Непрерывность функции в точке и на промежутке

Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.

Функция f (x) является непрерывной в точке x 0 , если предел слева равен пределу справа и совпадает со значением функции в точке x 0 , т.е.: lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) = f (x 0)

Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.

Пример 1

Дана функция f (x) = 1 6 (x - 8) 2 - 8 . Необходимо доказать ее непрерывность в точке х 0 = 2 .

Решение

В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов х n , сводящуюся к х 0 = 2 · (х n < 2) . Например, такой последовательностью может быть:

2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2

Соответствующая последовательность значений функций выглядит так:

f (- 2) ; f (0) ; f (1) ; f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16 ; . . . ; f 1 1023 1024 ; . . . = = 8 . 667 ; 2 . 667 ; 0 . 167 ; - 0 . 958 ; - 1 . 489 ; - 1 . 747 ; - 1 . 874 ; . . . ; - 1 . 998 ; . . . → - 2

на чертеже они обозначены зеленым цветом.

Достаточно очевидно, что такая последовательность сводится к - 2 , значит lim x → 2 - 0 1 6 (x - 8) 2 - 8 = - 2 .

Определим существование предела справа: используем последовательность аргументов х n , сводящуюся к х 0 = 2 (х n > 2) . Например, такой последовательностью может быть:

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Соответствующая последовательность функций:

f (6) ; f (4) ; f (3) ; f 2 1 2 ; f 2 1 4 ; f 2 1 8 ; f 2 1 16 ; . . . ; f 2 1 1024 ; . . . = = - 7 . 333 ; - 5 . 333 ; - 3 . 833 ; - 2 . 958 ; - 2 . 489 ; - 2 . 247 ; - 2 . 247 ; - 2 . 124 ; . . . ; - 2 . 001 ; . . . → - 2

на рисунке обозначена синим цветом.

И эта последовательность сводится к - 2 , тогда lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2 .

Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f (x) = 1 6 x - 8 2 - 8 в точке х 0 = 2 , при этом lim x → 2 1 6 (x - 8) 2 - 8 = - 2 .

После вычисления значения функции в заданной точке очевидно выполнение равенства:

lim x → 2 - 0 f (x) = lim x → 2 + 0 f (x) = f (2) = 1 6 (2 - 8) 2 - 8 = - 2 что свидетельствует о непрерывности заданной функции в заданной точке.

Покажем графически:

Ответ: Непрерывность функции f (x) = 1 6 (x - 8) 2 - 8 в заданной части доказано.

Устранимый разрыв первого рода

Функция имеет устранимый разрыв первого рода в точке х 0 , когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:

lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) ≠ f (x 0)

Пример 2

Задана функция f (x) = x 2 - 25 x - 5 . Необходимо определить точки ее разрыва и определить их тип.

Решение

Сначала обозначим область определения функции: D (f (x)) ⇔ D x 2 - 25 x - 5 ⇔ x - 5 ≠ 0 ⇔ x ∈ (- ∞ ; 5) ∪ (5 ; + ∞)

В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. х 0 = 5 . Исследуем функцию на непрерывность в этой точке.

Выражение x 2 - 25 x - 5 упростим: x 2 - 25 x - 5 = (x - 5) (x + 5) x - 5 = x + 5 .

Определим пределы справа и слева. Поскольку функция g (x) = x + 5 является непрерывной при любом действительном x , тогда:

lim x → 5 - 0 (x + 5) = 5 + 5 = 10 lim x → 5 + 0 (x + 5) = 5 + 5 = 10

Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.

Неустранимый разрыв первого рода также определяется точкой скачка функции.

Определение 3 Пример 3

Задана кусочно-непрерывная функция f (x) = x + 4 , x < - 1 , x 2 + 2 , - 1 ≤ x < 1 2 x , x ≥ 1 . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.

Решение

Разрывы данной функции могут быть лишь в точке х 0 = - 1 или в точке х 0 = 1 .

Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:

• слева от точки х 0 = - 1 заданная функция есть f (x) = x + 4 , тогда в силу непрерывности линейной функции: lim x → - 1 - 0 f (x) = lim x → - 1 - 0 (x + 4) = - 1 + 4 = 3 ;
• непосредственно в точке х 0 = - 1 функция принимает вид: f (x) = x 2 + 2 , тогда: f (- 1) = (- 1) 2 + 2 = 3 ;
• на промежутке (- 1 ; 1) заданная функция есть: f (x) = x 2 + 2 . Опираясь на свойство непрерывности квадратичной функции, имеем: lim x → - 1 + 0 f (x) = lim x → - 1 + 0 (x 2 + 2) = (- 1) 2 + 2 = 3 lim x → 1 - 0 f (x) = lim x → 1 - 0 (x 2 + 2) = (1) 2 + 2 = 3
• в точке х 0 = - 1 функция имеет вид: f (x) = 2 x и f (1) = 2 · 1 = 2 .
• справа от точки х 0 заданная функция есть f (x) = 2 x . В силу непрерывности линейной функции: lim x → 1 + 0 f (x) = lim x → 1 + 0 (2 x) = 2 · 1 = 2

Ответ: в конечном счете мы получили:

• lim x → - 1 - 0 f (x) = lim x → - 1 + 0 f (x) = f (- 1) = 3 - это означает, что в точке х 0 = - 1 заданная кусочная функция непрерывна;
• lim x → - 1 - 0 f (x) = 3 , lim x → 1 + 0 f (x) = 2 - таким образом, в точке х 0 = 1 определён неустранимый разрыв первого рода (скачок).

Нам остается только подготовить чертеж данного задания.

Функция имеет разрыв второго рода в точке х 0 , когда какой-либо из пределов слева lim x → x 0 - 0 f (x) или справа lim x → x 0 + 0 f (x) не существует или бесконечен.

Пример 4

Задана функция f (x) = 1 x . Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.

Решение

Запишем область определения функции: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) .

Найдем пределы справа и слева от точки х 0 = 0 .

Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:

8 ; - 4 ; - 2 ; - 1 ; - 1 2 ; - 1 4 ; . . . ; - 1 1024 ; . . .

Ей соответствует последовательность значений функции:

f (- 8) ; f (- 4) ; f (- 2) ; f (- 1) ; f - 1 2 ; f - 1 4 ; . . . ; f - 1 1024 ; . . . = = - 1 8 ; - 1 4 ; - 1 2 ; - 1 ; - 2 ; - 4 ; . . . ; - 1024 ; . . .

Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда lim x → 0 - 0 f (x) = lim x → 0 - 0 1 x = - ∞ .

Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х 0 справа. К примеру: 8 ; 4 ; 2 ; 1 ; 1 2 ; 1 4 ; . . . ; 1 1024 ; . . . , и ей соответствует последовательность значений функции:

f (8) ; f (4) ; f (2) ; f (1) ; f 1 2 ; f 1 4 ; . . . ; f 1 1024 ; . . . = = 1 8 ; 1 4 ; 1 2 ; 1 ; 2 ; 4 ; . . . ; 1024 ; . . .

Эта последовательность - бесконечно большая положительная, а значит lim x → 0 + 0 f (x) = lim x → 0 + 0 1 x = + ∞ .

Ответ : точка х 0 = 0 - точка разрыва функции второго рода.

Проиллюстрируем:

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних - правого и левого, которые совсем не страшны, несмотря на то что записываются как и .

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.

Графически функция непрерывна в точке , если её график не "разрывается" в этой точке. График такой непрерывной функции - показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

1. Функция определена в точке .

Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 - на рисунке ниже.

Пример 1. Функция f (x ) определена следующим образом:

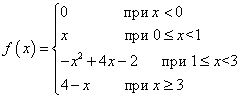
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0 , x = 1 , x = 3 ?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0 . Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0 .

Точка x = 1 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1 .

Точка x = 3 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3 .

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Что такое непрерывное изменение функции?

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m , то есть l = f (m ) , m ≥0 .

Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l . Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f (m ) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f (m ) непрерывна, а в точке она имеет разрыв.

Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика .

Непрерывность функции на промежутке

Пусть функция y = f (x ) определена в интервале ]a , b [ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a , b [ . Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b [ , ]a , + ∞[ , ]- ∞, + ∞[ . Пусть теперь функция y = f (x ) определена на отрезке [a , b ] . Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a , оставаясь на отрезке [a , b ] , мы можем приближаться только справа, а к точке b - только слева. Функция называется непрерывной на отрезке [a , b ] , если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b .

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a , b ] , функция непрерывна на отрезке [0 , b ] , функция непрерывна на любом отрезке, не содержащем точку a = 2 .

Пример 4. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках - 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение.

Найдём правосторонний предел при :

.

Очевидно, что значение в точке x = 2 должно быть равно ax :

a = 1,5 .

Пример 6. Определить, при каких значениях параметров a и b непрерывна на всей области определения функция

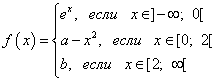
Решение.
Найдём левосторонний предел функции в точке :

.

Следовательно, значение в точке должно быть равно 1:

Найдём левосторонний функции в точке :

Очевидно, что значение функции в точке должно быть равно :

Ответ: функция непрерывна на всей области определения при a = 1; b = -3 .

Основные свойства непрерывных функций

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t , выраженная законом s = f (t ) , даёт пример непрерывной функции f (t ) . Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f (t ) .

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f (x ) , непрерывная на интервале [a , b ] , принимает все промежуточные значения между значениями в концевых точках, то есть, между f (a ) и f (b ) . В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

Определение непрерывности по Гейне

Говорят, что функция действительного переменного \(f\left(x \right)\) является непрерывной в точке \(a \in \mathbb{R}\) (\(\mathbb{R}-\)множество действительных чисел), если для любой последовательности \(\left\{ {{x_n}} \right\}\), такой, что \[\lim\limits_{n \to \infty } {x_n} = a,\] выполняется соотношение \[\lim\limits_{n \to \infty } f\left({{x_n}} \right) = f\left(a \right).\] На практике удобно использовать следующие \(3\) условия непрерывности функции \(f\left(x \right)\) в точке \(x = a\) (которые должны выполняться одновременно):

1. Функция \(f\left(x \right)\) определена в точке \(x = a\);
2. Предел \(\lim\limits_{x \to a} f\left(x \right)\) существует;
3. Выполняется равенство \(\lim\limits_{x \to a} f\left(x \right) = f\left(a \right)\).

Определение непрерывности по Коши (нотация \(\varepsilon - \delta\))

Рассмотрим функцию \(f\left(x \right)\), которая отображает множество действительных чисел \(\mathbb{R}\) на другое подмножество \(B\) действительных чисел. Говорят, что функция \(f\left(x \right)\) является непрерывной в точке \(a \in \mathbb{R}\), если для любого числа \(\varepsilon > 0\) существует число \(\delta > 0\), такое, что для всех \(x \in \mathbb{R}\), удовлетворяющих соотношению \[\left| {x - a} \right| Определение непрерывности в терминах приращений аргумента и функции

Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке \(x = a\), если справедливо равенство \[\lim\limits_{\Delta x \to 0} \Delta y = \lim\limits_{\Delta x \to 0} \left[ {f\left({a + \Delta x} \right) - f\left(a \right)} \right] = 0,\] где \(\Delta x = x - a\).

Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.

Функция является непрерывной на данном интервале , если она непрерывна в каждой точке этого интервала.

Теоремы непрерывности

Теорема 2.
Даны две функции \({f\left(x \right)}\) и \({g\left(x \right)}\), непрерывные в точке \(x = a\). Тогда сумма этих функций \({f\left(x \right)} + {g\left(x \right)}\) также непрерывна в точке \(x = a\).

Теорема 3.
Предположим, что две функции \({f\left(x \right)}\) и \({g\left(x \right)}\) непрерывны в точке \(x = a\). Тогда произведение этих функций \({f\left(x \right)} {g\left(x \right)}\) также непрерывно в точке \(x = a\).

Теорема 4.
Даны две функции \({f\left(x \right)}\) и \({g\left(x \right)}\), непрерывные при \(x = a\). Тогда отношение этих функций \(\large\frac{{f\left(x \right)}}{{g\left(x \right)}}\normalsize\) также непрерывно при \(x = a\) при условии, что \({g\left(a \right)} \ne 0\).

Теорема 5.
Предположим, что функция \({f\left(x \right)}\) является дифференцируемой в точке \(x = a\). Тогда функция \({f\left(x \right)}\) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).

Теорема 6 (Теорема о предельном значении).
Если функция \({f\left(x \right)}\) непрерывна на закрытом и ограниченном интервале \(\left[ {a,b} \right]\), то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа \(m\) и \(M\), такие, что \ для всех \(x\) в интервале \(\left[ {a,b} \right]\) (рисунок 1).

Непрерывность элементарных функций

Все элементарные функции являются непрерывными в любой точке свой области определения.

Функция называется элементарной , если она построена из конечного числа композиций и комбинаций
(с использованием \(4\) действий - сложение, вычитание, умножение и деление) . Множество основных элементарных функций включает в себя:

Лекция 4.

Непрерывность функций

1. Непрерывность функции в точке

Определение 1. Пусть функция y =f (x ) определена в точке х 0 и в некоторой окрестности этой точки. Функция y =f (x ) называется непрерывной в точке х 0 , если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

Таким образом, условие непрерывности функции y =f (x ) в точке х 0 состоит в том, что:

Так как
, то равенство (32) можно записать в виде

(33)

Это означает, что при нахождении предела непрерывной функции f (x ) можно перейти к пределу под знаком функции, т.е. в функцию f (x ) вместо аргумента х подставить его предельное значение х 0 .

lim sin x =sin(lim x );

lim arctg x =arctg (lim x ); (34)

lim lоg x =lоg (lim x ).

Задание. Найти предел: 1) ; 2)
.

Дадим определение непрерывности функции, опираясь на понятия приращения аргумента и функции.

Т.к. условия и
одинаковы (рис.4), то равенство (32) принимает вид:

или
.

Определение 2. Функция y =f (x ) называется непрерывной в точке х 0 , если она определена в точке х 0 и её окрестности, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Задание. Исследовать на непрерывность функцию y =2х 2 1.

Свойства функций, непрервных в точке

1. Если функции f (x ) и φ (x ) непрерывны в точке х 0 , то их сумма
, произведение
и частное
(при условии
) являются функциями, непрерывными в точке х 0 .

2. Если функция у =f (x ) непрерывна в точке х 0 и f (x 0)>0, то существует такая окрестность точки х 0 , в которой f (x )>0.

3. Если функция у =f (u ) непрерывна в точке u 0 , а функция u=φ (x ) непрерывна в точке u 0 =φ (x 0 ), то сложная функция y =f [φ (x )] непрерывна в точке х 0 .

2. Непрерывность функции в интервале и на отрезке

Функция y =f (x ) называется непрерывной в интервале (a ; b ), если она непрерывна в каждой точке этого интервала.

Функция y =f (x ) называется непрерывной на отрезке [a ; b ], если она непрерывна в интервале (a ; b ), и в точке х =а непрерывна справа (т.е. ), а в точке x =b непрерывна слева (т.е.
).

3. Точки разрыва функции и их классификация

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Если х =х 0  точка разрыва функции y =f (x ), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции.

Пример.

1.
. 2.

3)
4)
.

▼Точка разрыва х 0 называется точкой разрыва первого рода функции y =f (x ), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
и
. При этом:

Величину |A 1 -A 2 | называют скачком функции в точке разрыва первого рода. ▲

▼Точка разрыва х 0 называется точкой разрыва второго рода функции y =f (x ), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности. ▲

Задание. Найти точки разрыва и выяснить их тип для функций:

1)
; 2)
.

4. Основные теоремы о непрерывных функциях

Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.

Теорема 1. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель не равен нулю).

Теорема 2. Пусть функции u =φ (x ) непрерывна в точке х 0 , а функция y =f (u ) непрерывна в точке u =φ (x 0 ). Тогда сложная функция f (φ (x )), состоящая из непрерывных функций, непрерывна в точке х 0 .

Теорема 3. Если функция y =f (x ) непрерывна и строго монотонна на [a ; b ] оси Ох , то обратная функция у =φ (x ) также непрерывна и монотонна на соответствующем отрезке [c ;d ] оси Оу.

Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

5. Свойства функций, непрерывных на отрезке

Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Следствие. Если функция непрерывна на отрезке, то она ограничена на отрезке.

Теорема Больцано-Коши. Если функция y =f (x ) непрерывна на отрезке [a ; b ] и принимает на его концах неравные значения f (a )=A и f (b )=B ,
, то каково бы ни было число С , заключённое между А и В, найдётся точка такая, что f (c )=C .

Геометрически теорема очевидна. Для любого числа С , заключённого между А и В , найдётся точка с внутри этого отрезка такая, что f (С )=C . Прямая у =С пересечёт график функции по крайней мере в одной точке.

Следствие. Если функция y =f (x ) непрерывна на отрезке [a ; b ] и принимает на его концах значения разных знаков, то внутри отрезка [a ; b ] найдётся хотя бы одна точка с , в которой функция y =f (x ) обращается в нуль: f (c )=0.

Геометрический смысл теоремы: если график непрерывной функции переходит с одной стороны оси Ох на другую, то он пересекает ось Ох .

Определение. Функция f(x), определенная в окрестности некоторой точки х 0 , называется непрерывной в точке х 0 , если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х 0 , но не является непрерывной в самой точке х 0 , то она называется разрывной функцией, а точка х 0 – точкой разрыва.

Пример непрерывной функции:

y

0 x 0 - x 0 x 0 + x

Пример разрывной функции:

Определение. Функция f(x) называется непрерывной в точке х 0 , если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство
.

Определение. Функция f(x) называется непрерывной в точке х = х 0 , если приращение функции в точке х 0 является бесконечно малой величиной.

f(x) = f(x 0) + (x)

где (х) – бесконечно малая при хх 0 .

Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х 0 функций – есть функция, непрерывная в точке х 0 .

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х 0 .

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х 0 , то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

Непрерывность некоторых элементарных функций.

1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

2) Рациональная функция
непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции sinиcosнепрерывны на своей области определения.

Докажем свойство 3 для функции y = sinx.

Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:

Действительно, имеется предел произведения двух функций
и
. При этом функция косинус – ограниченная функция прих0
, а т.к.

предел функции синус
, то она является бесконечно малой прих0.

Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х 0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.

Точки разрыва и их классификация.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х 0 , за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х 0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

, то функция называется непрерывной справа.

Если односторонний предел (см. выше)
, то функция называется непрерывной слева.

Определение. Точка х 0 называется точкой разрыва функции f(x), если f(x) не определена в точке х 0 или не является непрерывной в этой точке.

Определение. Точка х 0 называется точкой разрыва 1- го рода , если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х 0 , достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х 0 называется точкой разрыва 2 – го рода , если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Непрерывность функции на интервале и на отрезке.

Определение. Функция f(x) называется непрерывной на интервале (отрезке) , если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

Свойства функций, непрерывных на отрезке.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке выполняется условие –M  f(x)  M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х 0 , ограничена в некоторой ее окрестности, а если разбивать отрезок на бесконечное количество отрезков, которые “стягиваются” к точке х 0 , то образуется некоторая окрестность точки х 0 .

Свойство 2: Функция, непрерывная на отрезке , принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х 1 и х 2 , что f(x 1) = m, f(x 2) = M, причем

m  f(x)  M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке , принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х 0 , то существует некоторая окрестность точки х 0 , в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a))  sign(f(b)), то  х 0: f(x 0) = 0.

Пример.

в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

у

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода